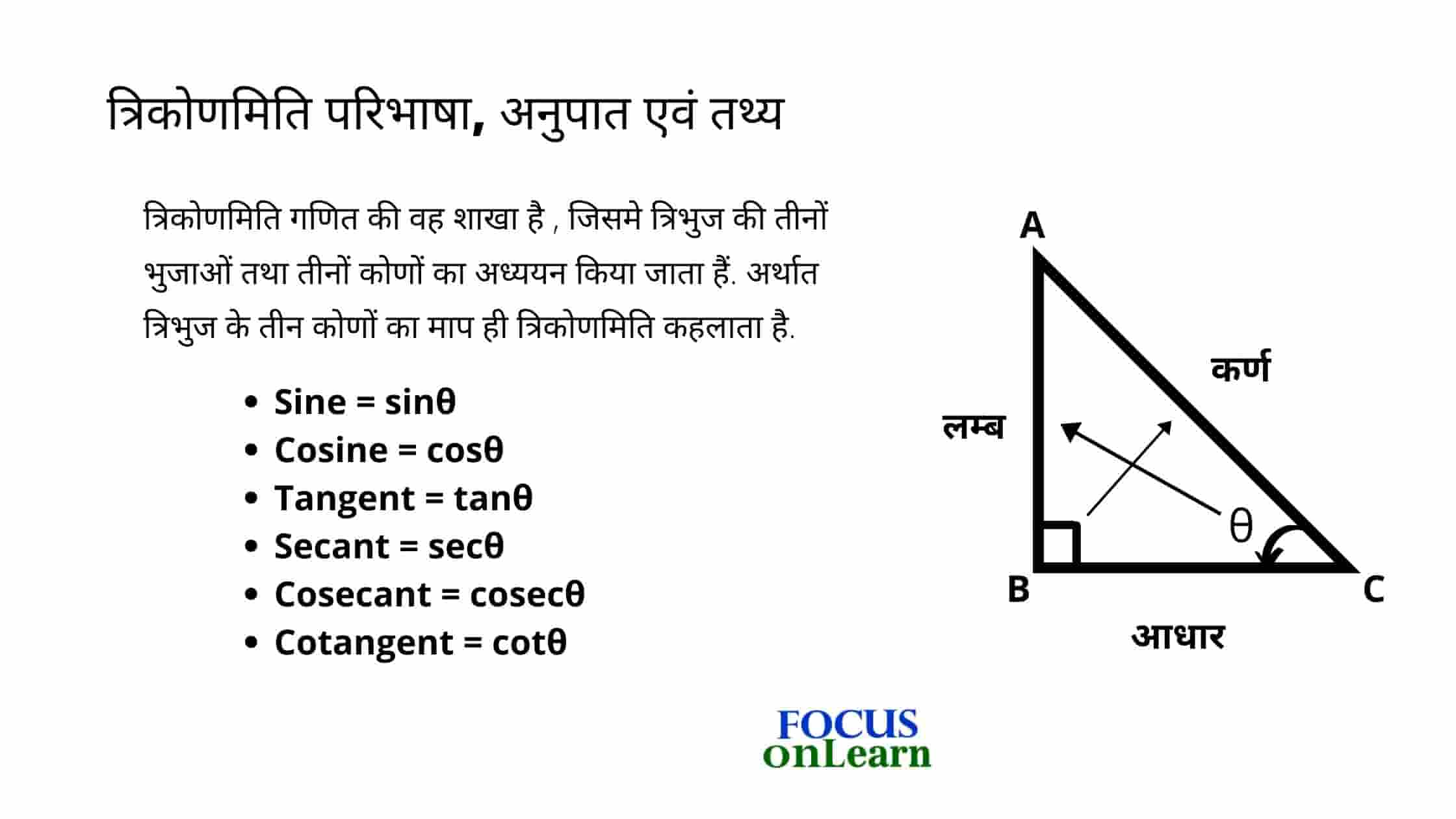
शंकु का क्षेत्रफल, वक्र पृष्ठीय एवं सम्पूर्ण पृष्ठीय क्षेत्रफल
शंकु को एक त्रिभुज के रूप में परिभाषित किया जा सकता है, हालांकि शंकु एक घुमावदार आकृति के रूप में होता है. वास्तव में, शंकु त्रि-आयामी एक ऐसी आकृति है जिसमें एक आधार पर सभी बिंदुओं को एक सामान्य बिंदु से जोड़ा जाता है. जहाँ शंकु का आधार वृताकार होता है. वही, Shanku ka Kshetrafal … Read more