समद्विबाहु त्रिभुज एक ऐसा गणितीय त्रिभुज है, जिसके दोनों भुजा एक दूसरे के बराबर होते हैं. साथ ही, इन समान भुजाओं के विपरीत कोण भी समान होते हैं. सामान्यतः त्रिभुज एक बहुभुज है, जिसमें तीन भुजाएँ, तीन शीर्ष और तीन कोण होते हैं. विशेष स्थिति में, त्रिभुज की भुजाएँ और कोण अलग-अलग हो सकते हैं, लेकिन Isosceles Triangle in Hindi में केवल दो भुजा और दो कोण होते बराबर होते है.
त्रिकोण यानि त्रिभुज के प्रकारों को भुजाओं एवं कोणों के आधार पर व्यक्त किया जाता है. जैसे; भुजाओं के आधार पर, त्रिभुज को तीन वर्गों में विभक्त किया जाता है; समबाहु, समद्विबाहु एवं विषमबाहु.
जबकि कोणों के आधार पर, त्रिभुज को तीन वर्गों में व्यक्त किया जाता है, न्यूनकोण, समकोण, एवं अधिककोण. समद्विबाहु त्रिभुज का सबसे अधिक प्रयोग क्लास 9th एवं 12th में होता है. जिसका सम्पूर्ण विवरण यानि समद्विबाहु त्रिभुज का फार्मूला, परिभाषा, एवं गुण यहाँ पढ़ेंगे.
समद्विबाहु त्रिभुज की परिभाषा
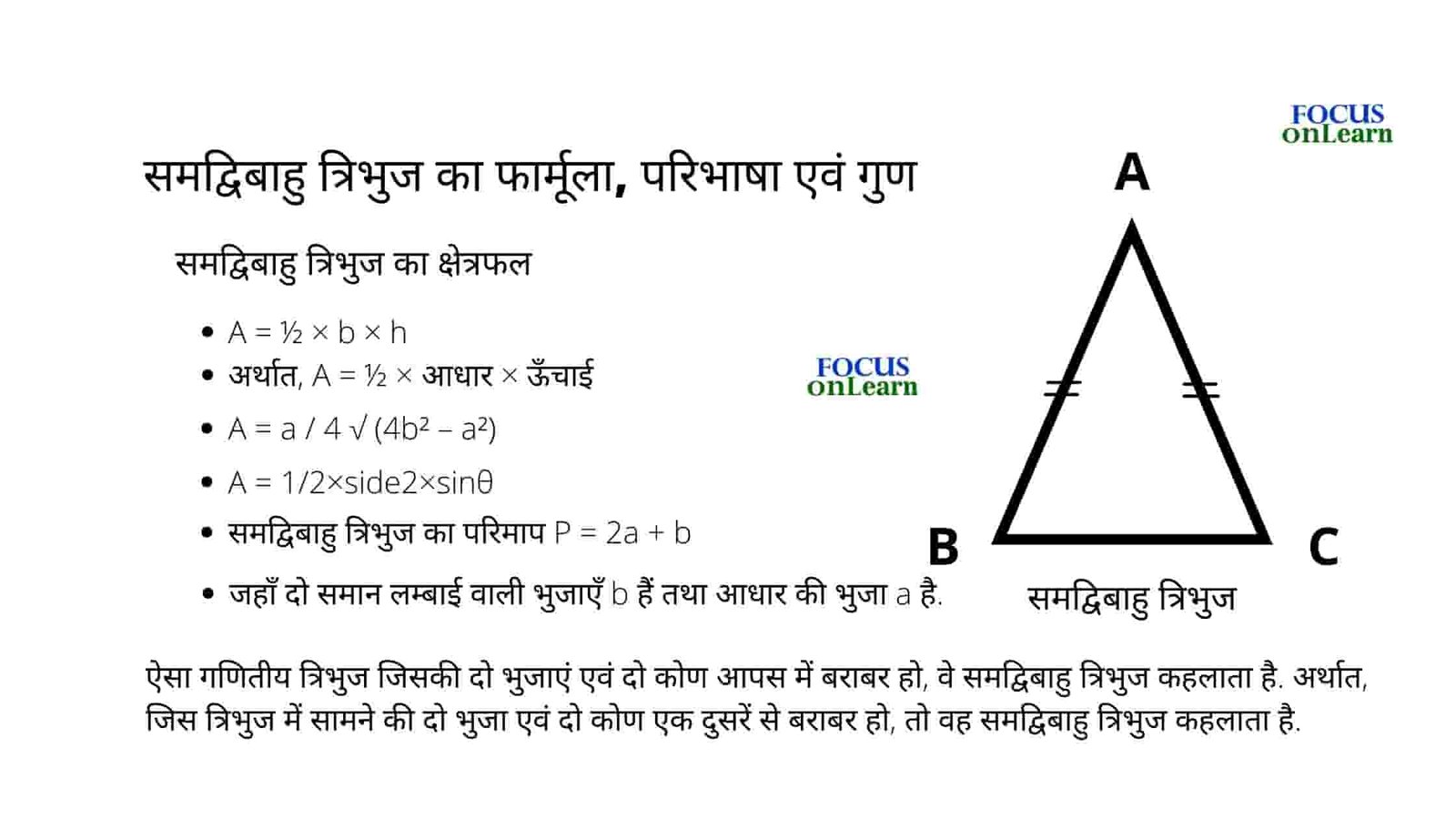
ऐसा गणितीय त्रिभुज जिसकी दो भुजाएं एवं दो कोण आपस में बराबर हो, वे समद्विबाहु त्रिभुज कहलाता है. अर्थात, जिस त्रिभुज में सामने की दो भुजा एवं दो कोण एक दुसरें से बराबर हो, तो वह समद्विबाहु त्रिभुज कहलाता है.
यदि विशेष स्थति में तीनों भुजाएँ समान लंबाई की हैं, तो वह समबाहु त्रिभुज कहा जाता है. स्पष्ट रूप से, समबाहु त्रिभुजों में समद्विबाहु त्रिभुज के सभी गुण निहित होते हैं.
परिभाषा को सरल बनाने के लिए समद्विबाहु त्रिभुज को निम्न भाग में विभक्त कर याद किया जा सकता है.
- सम = बराबर
- द्वि = दो
- बाहु = भुजा
अर्थात, समान लम्बाई की दो भुजा = समद्विबाहु त्रिभुज
अवश्य पढ़े, श्रेढ़ी का महत्वपूर्ण फार्मूला
समद्विबाहु त्रिभुज की गुणधर्म
- समद्विबाहु त्रिभुज की दो भुजाएं आपस में बराबर होती हैं.
- शेष यानि तीसरी भुजा को आधार आधार कहा जाता है.
- त्रिभुज के दो समान भुजाओं के विपरीत कोण हमेशा एक दुसरें से समान होते हैं.
- बराबर भुजाओं के सामने के कोण बराबर होते हैं.
- शीर्ष से आधार पर डाला गया लम्बवत रेखा आधार को समद्विभाजित करती है.
- आधार का पर डाला गया लम्ब शीर्ष से होकर जाता है.
- एक समद्विबाहु त्रिभुज में 90 डिग्री के रूप में तीसरा कोण उपलब्ध होता है.
- आधार का लम्बार्द्धक शीर्ष कोण को समान भागो में विभाजित करता है.
- समद्विबाहु त्रिभुज का असमान भुजा, त्रिभुज के आधार के रूप में होता है.
- ऊँचाई, आधार से ऊपरी शीर्ष पर लंबवत दूरी है.
समद्विबाहु त्रिभुज का फार्मूला
इस त्रिभुज में निम्न फार्मूला होते है जो इस प्रकार है.
1. समद्विबाहु त्रिभुज का क्षेत्रफल A = ½ × b × h अर्थात, A = ½ × आधार × ऊँचाई
2. दूसरा क्षेत्रफल A = a / 4 √ (4b² – a²)
3. तीसरा क्षेत्रफल A = 1/2×side2×sinθ जहाँ θ = थीटा, जो त्रिभुज का कोण है.
4. समद्विबाहु त्रिभुज का परिमाप P = 2a + b
जहाँ दो समान लम्बाई वाली भुजाएँ b हैं तथा आधार की भुजा a है.
अवश्य पढ़े,
- अलजेब्रा का महत्वपूर्ण फार्मूला
- द्विघात समीकरण फार्मूला
- रैखिक समीकरण का हल एवं प्रकार
- बहुपद का फार्मूला
समद्विबाहु त्रिभुज के महत्वपूर्ण तथ्य
सामान्यतः Isosceles Triangle in Hindi के फार्मूला का प्रयोग कर आधार, उचाई एवं कोण ज्ञात किया जा सकता है. इसमें पाइथागोरस प्रमेय का उपयोग कर सभी प्रश्नों को सरल बनाया जा सकता है. जैसा की आप जानते है कि प्रत्येक त्रिभुज के कोणों का माप 180 डिग्री होता है.
लेकिन, यदि किसी त्रिभुज में कोण नही दिया गया हो, तो A = 1/2×side2×sinθ फार्मूला प्रयोग कोण भी सरलता से प्राप्त कर सकते है. इस टॉपिक में कोई संदेह या सुझाव हो, तो हमें कमेंट अवश्य करे.
सामन्य प्रश्न FAQs
Q. समद्विबाहु त्रिभुज का परिमाप सूत्र?
समद्विबाहु त्रिभुज का परिमाप का सूत्र p = 2a + b होता है. इस फार्मूला का प्रयोग समद्विबाहु का परिमाप निकालने के लिए किया जाता है.
Q. समद्विबाहु त्रिभुज का क्षेत्रफल क्या होता है?
समद्विबाहु त्रिभुज का क्षेत्रफल 1/2 x आधार x ऊँचाई होता है. अर्थात, इस फार्मूला का उपयोग सम्पूर्ण भाग का क्षेत्रफल निकालने के लिए होता है.
Q. समद्विबाहु त्रिभुज का आधार क्या है?
एक समद्विबाहु त्रिभुज की तीसरी भुजा जो अन्य दो भुजाओं के असमान होती है, उसे समद्विबाहु त्रिभुज का आधार कहलाती है.