समकोण त्रिभुज का क्षेत्रफल, परिभाषा और गुण

सामान्तः ज्यामिति में, Samkon Tribhuj एक नियमित बहुभुज होता है, जिसमें तीन भुजाएँ एवं तीन कोण होती हैं और किसी भी दो भुजाओं का योग हमेशा तीसरी भुजा से अधिक होती है. यह त्रिभुज की एक विशेष स्थिति है. भुजाओं एवं कोणों के आधार पर त्रिभुज भी अलग-अलग भाग होते है. जैसे; समबाहु, समद्विबाहु, आदि.

तीन भुजाओं से घिरी हुई बंद आकृति का योग 180° के बराबर होता है जो सभी तीन आंतरिक कोणों का योग है. समकोण त्रिभुज के सम्बन्ध में इन्ही प्रक्रियाओं एवं सूत्रों पर विशेष रूप से चर्चा निचे किया गया है. जिसमे फार्मूला के साथ-साथ परिभाषा, एवं इसके गुण भी सामिल है.

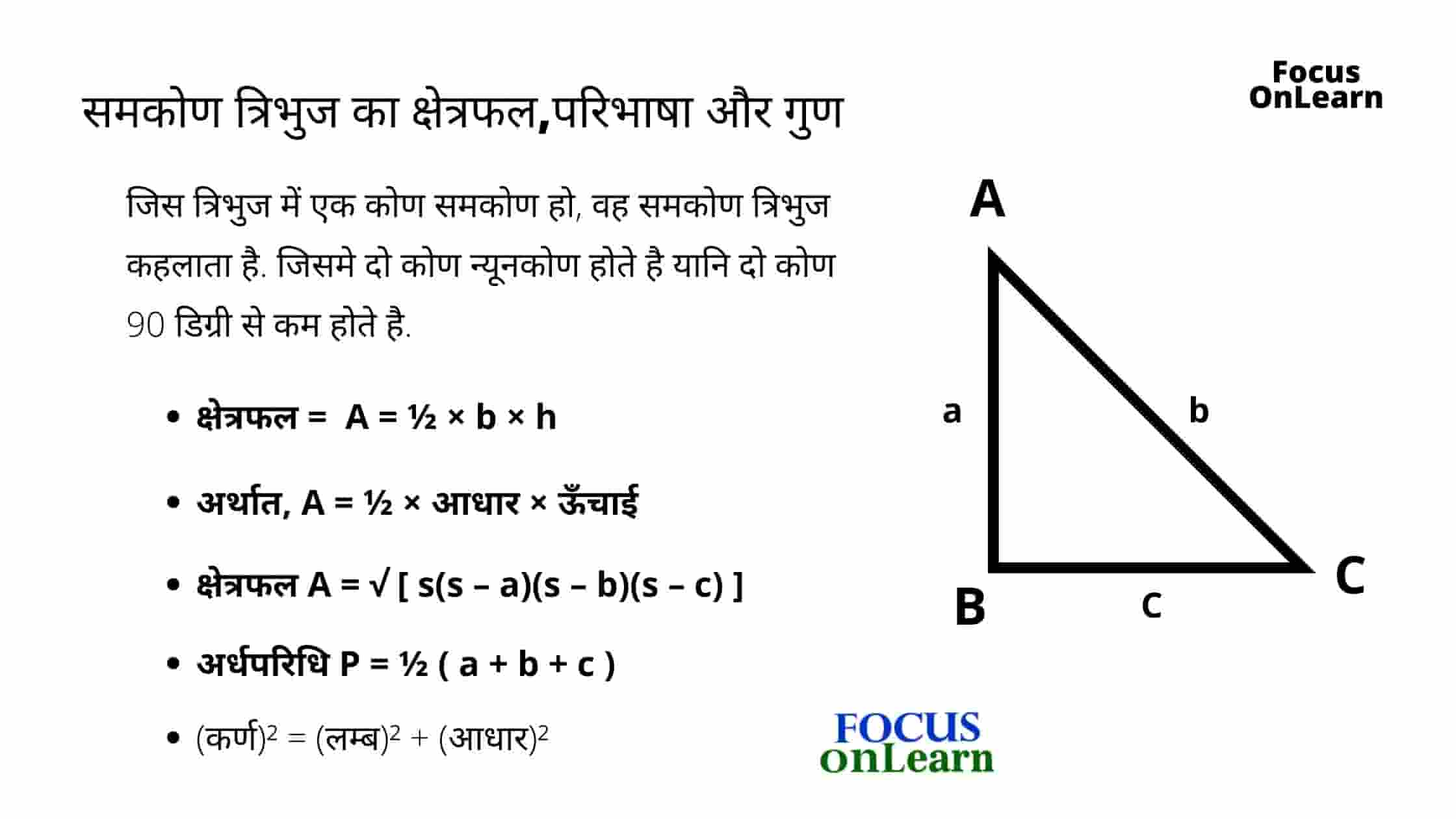
समकोण त्रिभुज किसे कहते है?

जिस त्रिभुज में एक कोण समकोण हो, वह समकोण त्रिभुज कहलाता है. जिसमे दो कोण न्यूनकोण होते है यानि दो कोण 90 डिग्री से कम होते है. सामान्यतः, इस कोण की व्याख्या इसके कोण की माप से की जाती है. क्योंकि दुनियां में कोई भी चित्र बनी है वो किसी न किसी त्रिभुज का भाग अवश्य है. अतः पहचान के लिए कोण आवश्यक है.

दुसरें शब्दों में, समकोण त्रिभुज वह त्रिभुज होता है जिसमें 3 भुजाएँ 90 डिग्री कोण के साथ स्थिर होती है. इस त्रिभुज के भुजाओं को आधार, कर्ण और ऊँचाई से सूचित किया जाता है जोआधार के साथ 90° का कोण बनाता है.

• कर्ण: 90° के सामने वाली भुजा को समकोण कहा जाता है.

• लम्ब: वैसी भुजा जो आधार के साथ 90 डिग्री का कोण बनाती हैं, उसे लम्ब कहा जाता है.

• आधार: समकोण त्रिभुज में शेष भुजा को आधार कहा जाता है.

अन्य महत्वपूर्ण त्रिभुज

• समद्विबाहु त्रिभुज का फार्मूला

• समबाहु त्रिभुज का परिभाषा एवं फार्मूला

• विषमबाहु त्रिभुज फार्मूला, परिभाषा एवं गुणधर्म

समकोण त्रिभुज का प्रकार

गणितज्ञों द्वारा समकोण त्रिभुज को प्रयोग के आधार पर मुख्यतः दो वर्गों में बाँता गया है. दोनों त्रिभुज भुजा एवं कोण को परिभाषित करते है. समकोण में भी भुजाओं एवं कोणों की एक अलग पहचान निर्धारित किया गया है जो इसकी व्याख्या करते है.

1. समद्विबाहु समकोण त्रिभुज
2. विषमबाहु समकोण त्रिभुज

समद्विबाहु समकोण त्रिभुज

वैसा समकोण त्रिभुज जिसमें दो भुजाएँ एवं दो कोण आपस में समान हो, तो वह समद्विबाहु समकोण त्रिभुज  कहलाता है. ऐसे त्रिभुज में दो कोण 45-45 डिग्री के होते है तथा शेष 90 डिग्री का होता है. सभी कोणों का माप 180 डिग्री होता है. जैसे;

• ∠A = 45°
• ∠B = 90°
• ∠C = 45°
• ∠A + ∠B + ∠C = 180°

इसे भी पढ़े, श्रेढ़ी का महत्वपूर्ण फार्मूला एवं ट्रिक्स

विषमबाहु समकोण त्रिभुज

वैसा समकोण त्रिभुज जिसके भुजाओं की लम्बाई अलग-अलग तथा कोणों की माप भी अलग-अलग होते है, उसे विषमबाहु समकोण त्रिभुज कहते है. इस त्रिभुज में एक कोण की माप 30° एवं दुसरें की 60° होती है. अर्थात,

• ∠A = 30°
• ∠B = 90°
• ∠C = 60°
• ∠A + ∠B + ∠C = 180°

समकोण त्रिभुज का फार्मूला: Samkon Tribhuj Ka Formula

सामान्यतः समकोण त्रभुज का क्षेत्रफल कई फार्मूला का प्रयोग करके भी प्राप्त किया जा सकता है. जिसमे सबसे प्रमुख सामान्य त्रिभुज है. जो लगभल प्रत्येक त्रिकोण में प्रयुक्त होता है.

समकोण त्रिभुज का क्षेत्रफल

क्षेत्रफल दो-आयामी क्षेत्र को कहा जाता है और इसे वर्ग इकाई में मापा जाता है. जिसे किसी ऑब्जेक्ट द्वारा ली गई अंतरिक्ष की मात्रा के रूप में परिभाषित किया जा सकता है.

1. क्षेत्रफल =  A = ½ × b × h अर्थात, A = ½ × आधार × ऊँचाई

क्षेत्रफल हेरोन के भी फार्मूला से भी ज्ञात किया जा सकता है. जैसे;

 2. क्षेत्रफल A =√ [ s(s – a)(s – b)(s – c) ]

जहाँ अर्धपरिधि P = ½ ( a + b + c ) तथा a, b, और c त्रिभुज की भुजाएँ है.

3. समकोण त्रिभुज का परिमाप = ( a + b + c )

Note:
पाईथागोरस या बोधायन प्रमेय के अनुसार समकोण इस प्रकार व्यक्त किया गया है.

कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है. अर्थात

(कर्ण)² = (लम्ब)² + (आधार)²

समकोण त्रिभुज का गुण

• दाहिने कोण से कर्ण तक एक लंब डालने पर तीन समान त्रिभुज प्राप्त होते है.
• इस त्रभुज में एक कोण हमेशा समकोण होता है.
• कर्ण हमेशा सबसे बड़ी भुजा होता है.
• अन्य दो आन्तरिक कोणों का योगफल 90 डिग्री होता है.
• आधार से सटे अन्य दो भुजा आधार और कर्ण होते है.
• कर्ण सबसे बड़ी भुजा है.

Note:

पाइथागोरस प्रमेय के अनुसार: यदि किसी त्रिभुज में सबसे लंबी भुजा का वर्ग, अन्य दो भुजाओं के वर्गों के योग के बराबर हो, तो वह एक समकोण त्रिभुज होता है. अर्थात, BC² = AC² + AB²

निष्कर्ष

सामान्यतः Samkon Tribhuj में, त्रिकोणमितीय फलन या पाइथागोरस प्रमेय का केवल इसकेतीसरी भुजा को ढूढ़ने के लिए किया जाता है. जब त्रिभुज में कोई कोण न दिया हो, तो Sin, cos और Tan का प्रयोग किया जाता है. लेकिन क्षेत्रफल ज्ञात करने के लिए त्रिभुज के सामान्य फार्मूला का प्रयोग किया जाता है. उम्मीद करता हूँ कि सभी संदेह ख़त्म हो गए होंगे.