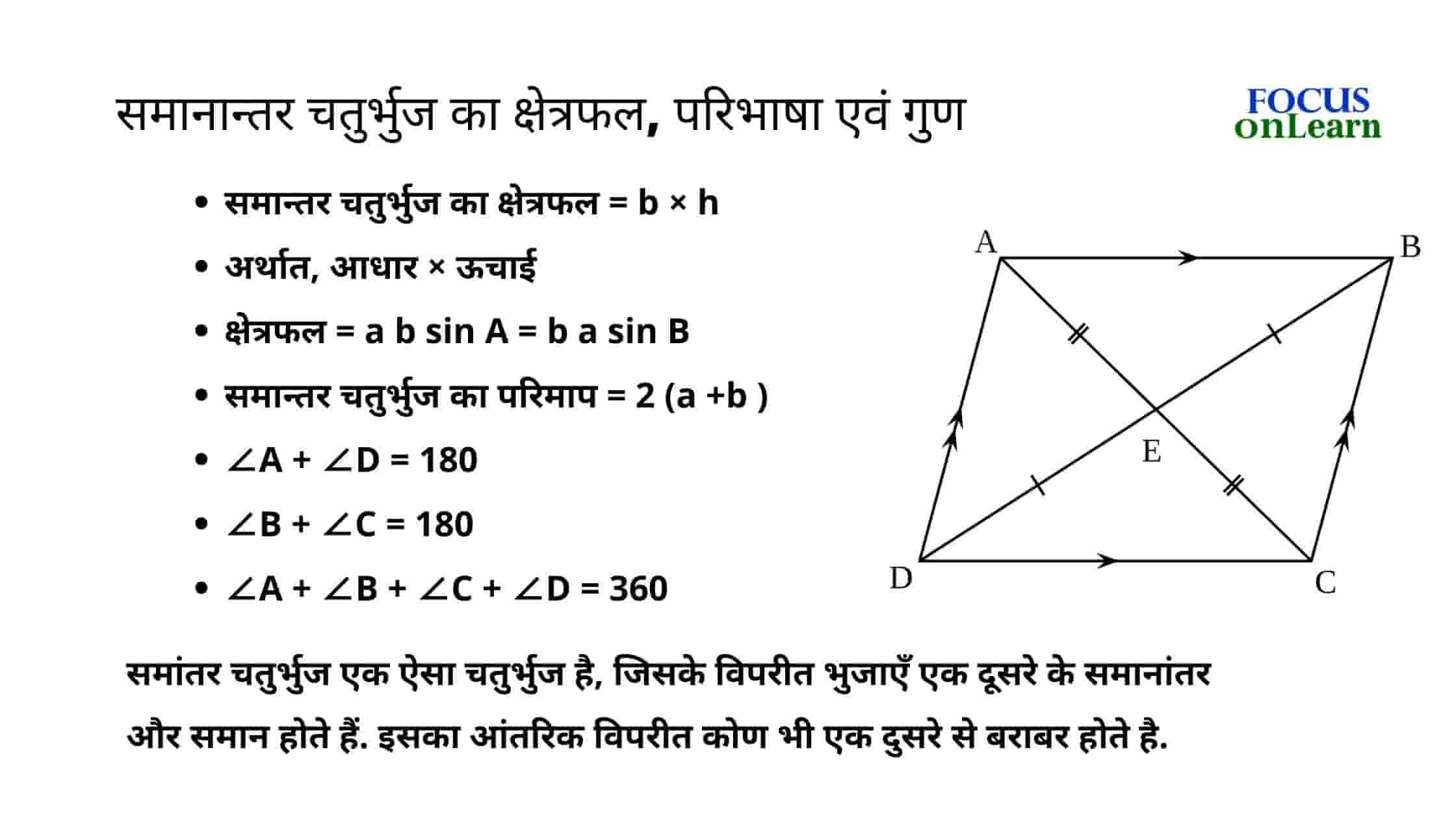
सामान्यतः समांतर चतुर्भुज एक द्वि-आयामी ज्यामितीय आकृति है जो दो समरूप भुजाओं से निर्मित है. अर्थात जिसके किनारे एक-दूसरे के समानांतर दो रेखाएं हैं. यह एक प्रकार का बहुभुज होता है जिसमे चार भुजाएँ एवं चार कोण होती हैं. samantar chaturbhuj के विकर्ण एक दुसरें को विभाजित करते है.
समानांतर भुजाओं की लम्बाई एक दुसरें से बराबर होती है, तथा इसके अलावा, एक समांतर चतुर्भुज के विपरीत कोण के माप बराबर होते हैं. साथ ही, समांतर कोण के समीपवर्ती कोणों का योग हमेशा 180 डिग्री के बराबर होता है. इस चतुर्भुज की परिभाषा, गुण एवं फार्मूला अत्यंत महत्वपूर्ण है जो प्रतियोगिता परीक्षा एवं बोर्ड एग्जाम में अच्छे मार्क्स दिलाने में मदद करता है.
समानान्तर चतुर्भुज किसे कहते है
जिस चतुर्भुज की आमने-सामने की भुजाएँ समांतर एवं समरूप हो, वह समान्तर चतुर्भुज चतुर्भुज कहलाता है.
दुसरें शब्दों में, समांतर चतुर्भुज एक ऐसा चतुर्भुज है, जिसके विपरीत भुजाएँ एक दूसरे के समानांतर और समान होते हैं. इसका आंतरिक विपरीत कोण भी एक दुसरे से बराबर होते है.
इसके अलावा, समानान्तर चतुर्भुज के ट्रांसवर्सल एक ही कोण पर 180 डिग्री तक या एक दूसरे के पूरक हैं, तथा सभी कोणों का योग 360 डिग्री के बराबर होते है.
समरूपता के अनुसार, एक वर्ग और एक आयत दो ऐसी आकृतियाँ हैं जिसमें समांतर चतुर्भुज के समान गुण होते हैं. यह समानान्तर चतुर्भुज के सामान्य गुण है.
अवश्य पढ़े, त्रिभुज के प्रकार और परिभाषा
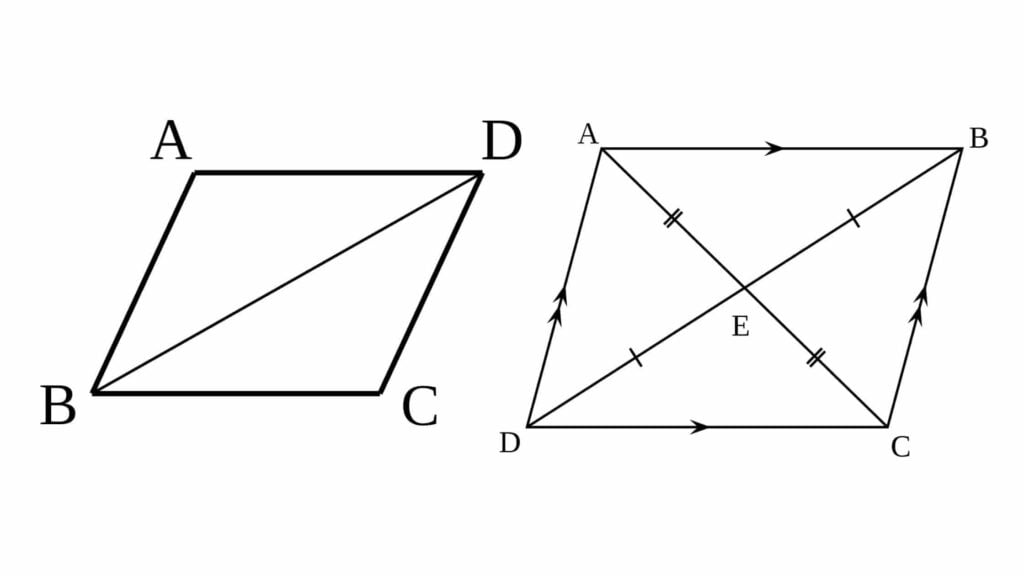
समानान्तर चतुर्भुज में
- भुजाओं की संख्या = 4
- शीर्षों की संख्या = 4
- समानांतर भुजाएँ = 2
- बहुभुज का प्रकार = चतुर्भुज
- ∠A + ∠D = 180
- ∠B + ∠C = 180
- ∠C + ∠D = 180
- ∠A + ∠B = 180
- भुजाएँ AD || BC
- तथा DC || AB
समान्तर चतुर्भुज का फार्मूला | Samantar Chaturbhuj
इस चतुर्भुज का फार्मूला महत्वपूर्ण होता है क्योंकि प्रश्न हल करने के लिए इसके क्षेत्रफल एवं परिमाप की आवश्यकता सबसे अधिक होता है. विशेषज्ञ मानते है कि क्लास 8 और 10 में इसपर आधारित बहुत सारें प्रश्न होते है. जो मुख्य रूप से इस फार्मूला से ही हल किए जाते है. इसलिए सभी आवश्यक फार्मूला यहाँ दिया गया है.
अवश्य पढ़े,
समान्तर चतुर्भुज का क्षेत्रफल | Samantar Chaturbhuj ka Kshetrafal
Samantar Chaturbhuj का क्षेत्रफल द्वि-आयामी विमाए में इसके द्वारा व्याप्त क्षेत्र है जो इसके भुजाओं के गुणनफल निकलता है. चतुर्भुज के क्षेत्रफल के लगभग सभी सूत्र समान्तर चतुर्भुज के लिए भी प्रयोग होता है. क्योंकि भाजाओं एवं कोण पर यह सभी के बराबर होता है.
समान्तर चतुर्भुज का क्षेत्रफल = b × h अर्थात, आधार × ऊचाई
दूसरा क्षेत्रफल = a b sin A = b a sin B
जहाँ a और b भुजाएँ तथा A और B कोण है.
Note: समान्तर चतुर्भुज को एक समलम्ब चतुर्भुज और एक समकोण त्रिभुज में विभक्त किया जा सकता है. उस स्थति में सूत्र लगभग समरूप हो सकते है.
समान्तर चतुर्भुज का परिमाप
किसी भी आकार की ज्यामितीय परिमाप आकृति के चारों ओर किसी भी आकार की कुल लंबाई होती है. समानान्तर चतुर्भुज में दोनों उचाई एवं दोनों आधार अलग-अलग आपस में बराबर होते है. गणितज्ञों के अनुसार ज्यामितीय आकृति के भुजाओं का योग ही परिमाप कहलाता है.
समान्तर चतुर्भुज का परिमाप = 2 (a +b ), जहाँ a और b चतुर्भुज के भुजाएँ है.
समान्तर चतुर्भुज की गुण
- आमने सामने की भुजाएं बराबर और समान्तर होती हैं.
- विकर्ण एक दूसरे को समद्विभाजित करते हैं.
- आमने सामने के कोण बराबर होते हैं.
- प्रत्येक आयत समान्तर चतुर्भुज होता है.
- विपरीत भुजाएँ समानांतर और सर्वांगसम होते हैं
- समांतर चतुर्भुज के विकणों के कोण बराबर होते हैं.
- प्रत्येक सम चतुभज समान्तर चतुर्भुज होता है.
- विपरीत कोण भी सर्वांगसम होते हैं.
- विकर्ण आमने सामने के कोण को समद्विभाजित करते हैं.
- प्रत्येक वर्ग समान्तर चतुर्भुज होता है.
- यदि कोणों में से कोई एक समकोण है, तो अन्य सभी कोण समकोण होता है.
- आयत व वर्ग को छोड़कर प्रत्येक समांतर चतुर्भुज के विकर्ण आपस में बराबर नहीं होते है.
पूछे जाने वला समान्य प्रश्न FAQs
Q. समांतर चतुर्भुज के क्षेत्रफल का सूत्र क्या होता है?
समांतर चतुर्भुज के क्षेत्रफल का आधार X ऊंचाई होता है.
Q. समांतर चतुर्भुज में कुल कितने गुण होते हैं?
समांतर चतुर्भुज के कुल चार गुण होते है, जिसकी सम्मुख भुजाएँ समान और समांतर होती हैं.