गणितीय ज्यामिति में, त्रिभुज सामान्यतः तीन भुजाओं और तीन कोणों के साथ एक बंद दो आयामी विमाए आकृति है. मुख्यतः त्रिभुज को त्रि-पक्षीय बहुभुज भी कहा जाता है. कोण के माप के आधार पर त्रिभुज तीन भागों में विभक्त होता है. जैसे, न्यूनकोण, समकोण, और अधिककोण. तीनों त्रिभुजों का अपना-अपना अगल गुणधर्म है जो इसे व्यक्त करते है.
त्रिभुज के भुजाओं और आंतरिक कोणों के आधार पर, विभिन्न प्रकार के त्रिकोण या त्रिभुज हो सकते हैं, उनमे से एक न्यूनकोण है. जिसका विस्तार से अध्ययन आप यहाँ करेंगे. न्यूनकोण से प्रतियोगिता एग्जाम में हमेशा अत्यधिक प्रश्न पूछा जाता है. इसलिए, इसके सभी आवश्यक फार्मूला, गुण और परिभाषा जानना आवश्यक है.
न्यूनकोण त्रिभुज किसे कहते हैं?
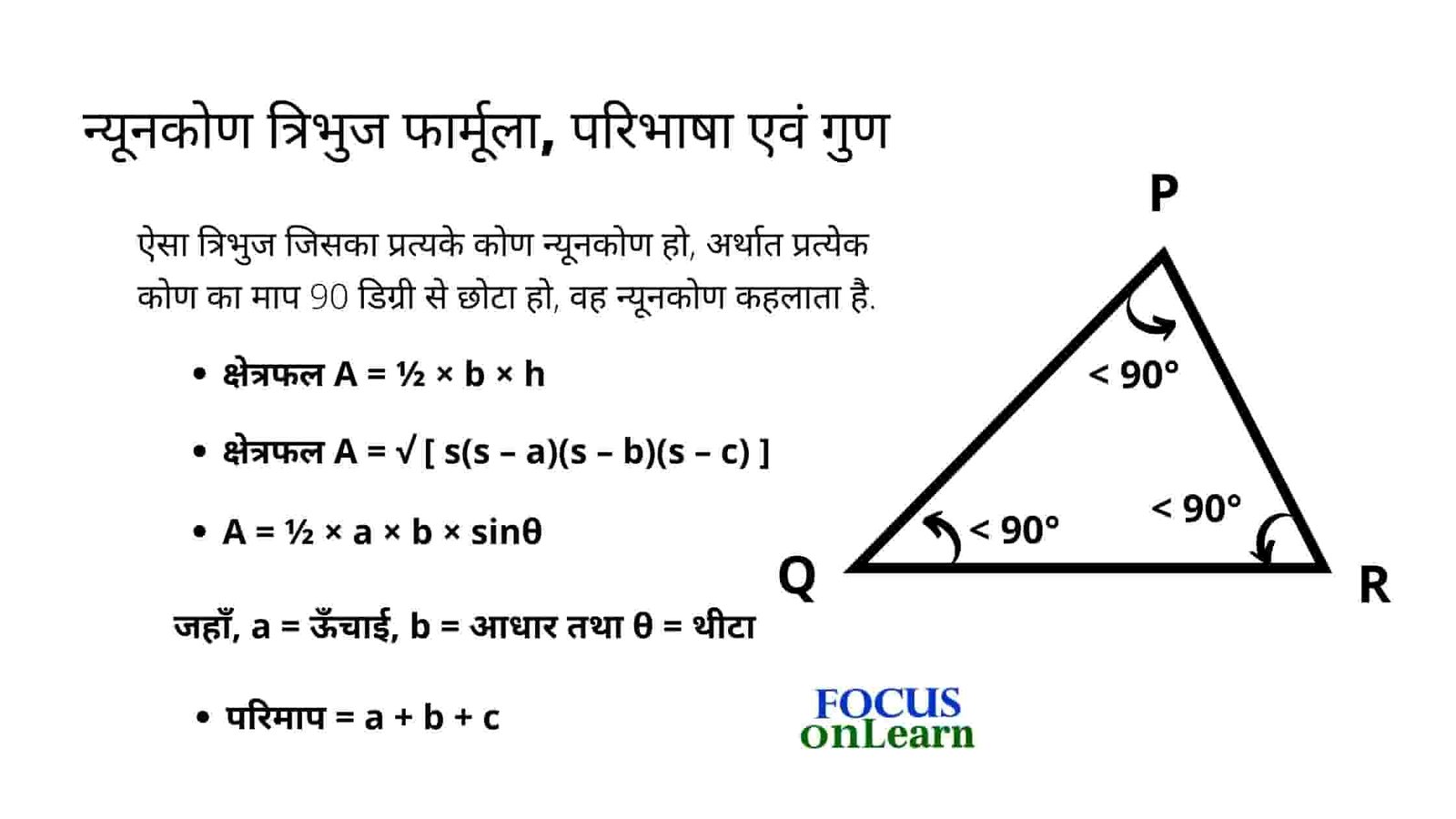
ऐसा त्रिभुज जिसका प्रत्यके कोण न्यूनकोण हो, अर्थात प्रत्येेक कोण का माप 90 डिग्री से छोटा हो, वह न्यूनकोण कहलाता है. यानि वैसा त्रिभुज जिसका कोई भी कोण 90 डिग्री से अधिक न हो, उसे न्यूनकोणकहते है. तीनों न्यूनकोणों का योग सदैव 180 डिग्री के बराबर होता है.
न्यूनकोण की परिभाषा भिन्न-भिन्न हो सकता है लेकिन अर्थ सदैव समान ही रहता है. क्योंकि परिभाषा स्मरण करने की उदेश्य से बनाया जाता है. जैसे;
∠ PQR एक न्यूनकोण है जिसमे,
∠PQR = ∠Q = 75°
∠PRQ = ∠R = 65°
∠QPR = ∠P = 40°
अन्य महत्वपूर्ण त्रिभुज
न्यूनकोण का फार्मूला
त्रिभुज का क्षेत्रफल और परिमाप निम्न फार्मूला का प्रयोग कर ज्ञात किया जा सकता है.
न्यूनकोण का क्षेत्रफल
1. न्यूनकोण का क्षेत्रफल A = ½ × b × h
जहाँ, b त्रिभुज का आधार है और,
h त्रिभुज की ऊंचाई
हेरॉन के सूत्र को प्रयोग कर न्यूनकोण का क्षेत्रफल निकला जाता है. जैसे,
2. अर्धपरिधि P = ½ ( a + b + c )
3. क्षेत्रफल A = √ [ s(s – a)(s – b)(s – c) ]
अगर दो भुजा और एक कोण दिया हो, तो निम्न फार्मूला का प्रयोग किया जाता है.
4. A = ½ × a × b × sinθ
जहाँ, a = ऊँचाई, b = आधार तथा θ = थीटा, जो त्रिभुज का कोण है.
अवश्य पढ़े,
न्यूनकोण का परिमाप
एक न्यूनकोण त्रिभुज के तीनों भुजाओं के लंबवत द्विभाजनों का अंतर परिधि का निर्माण करता है, जो हमेशा त्रिभुज के अंदर स्थित होता है. निम्न फार्मूला का प्रयोग कर मान निकला जाता है.
परिमाप = a + b + c
न्यूनकोण त्रिभुज का गुण
- न्यूनकोण त्रिभुज में दो भुजाओ के वर्गो का योग सदैव तीसरी भुजा के वर्ग से बड़ा होता है.
- लंबवत द्विभाजक एक खंड है.
- त्रिभुज में आंतरिक कोण हमेशा अलग-अलग उपायों के साथ 90° से कम होता है.
- न्यूनकोण त्रिभुज में सदैव दो कोणों का योग 90° से अधिक होता है.
- समबाहु त्रिभुज न्यूनकोण हो सकता है.
- तीनों कोणों का माप 180 डिग्री होता है.
- न्यूनकोण को समद्विबाहु त्रिभुज और समबाहु त्रिभुज के रूप में वर्गीकृत किया जा सकता है.
निष्कर्ष
अगर त्रिभुज के सभी कोण 60 ° हो, तो यह एक विशेष त्रिभुज बनाता है जिसे समबाहु त्रिभुज कहा जाता है. ऐसे स्थिति समद्विबाहु त्रिभुज के साथ भी हो सकता है. अर्थात न्यूनकोण समबाहु या समद्विबाहु त्रिभुज में परिवर्तित हो सकता है. Acute Angle Triangle in Hindi का प्रयोग मुख्य रूप से क्लास 6 से लेकर PhD तक किया जाता है. इसलिए, इसका महत्व अधिक है.