घन का क्षेत्रफल घन के सभी सतहों द्वारा घिरे हुए क्षेत्रों का योग होता है, जो इसे पुर्णतः कवर करता है. फार्मूला के अनुसार Ghan ka Kshetrafal के किनारों की लंबाई के वर्ग के छह गुना के बराबर होता है. हालांकि सूत्र का प्रयोग स्थति के अनुसार अलग-अलग रूप में हो सकते है. जैसे क्षेत्रफल से भुजा निकलना, भुजा से क्षेत्रफल आदि.
जब कभी भी किसी घन को त्रिविमीय आकृति में रखा जाता है, तो घन के किनारों द्वारा घिरा हुआ क्षेत्र घन का पृष्ठीय क्षेत्रफल कहलाता है. ऐसे क्षेत्र को घन के आयतन और क्षेत्रफल में परिभाषित किया जा सकता है.
यह ऐसी आकृति है जिसका प्रयोग बोर्ड और प्रतियोगिता में प्रश्न के लिए होता है. इसलिए, क्लास 10, क्लास 12, एसएससी, रेलवे, आदि जैसे एग्जाम में इससे प्रश्न पूछा जाता है. यहाँ सभी महत्वपूर्ण क्षेत्रफल दिया गया है जो एग्जाम में सहायता करते है.
घन का पृष्ठीय क्षेत्रफल का परिभाषा
6 वर्गाकार सतह से बना वह त्रिविमीय आकृति, जिसमे प्रत्येक तीन संलग्न सतहें एक-दुसरें पर लम्बवत हो, वह घन कहलाते है.
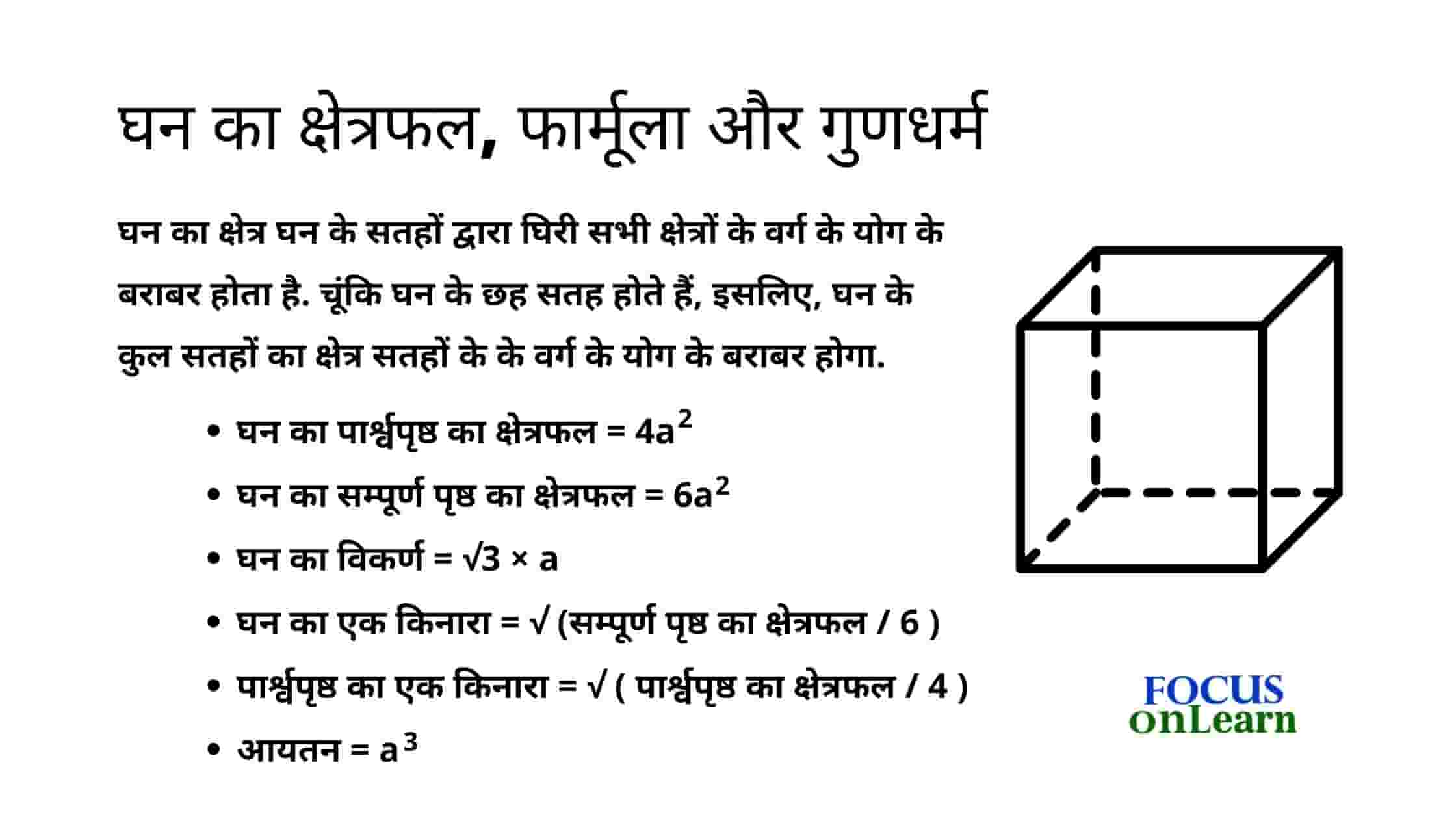
घन का क्षेत्र घन के सतहों द्वारा घिरी सभी क्षेत्रों के वर्ग के योग के बराबर होता है. चूंकि घन के छह सतह होते हैं, इसलिए, घन के कुल सतहों का क्षेत्र सतहों के वर्ग के योग के बराबर होगा.
अर्थात, क्षेत्रफल = a2 + a2 + a2 + a2 + a2 +a2 = 6a2 वर्ग इकाई.
Note: क्षेत्रफल को हमेशा वर्ग इकाई में ही मापा जाता है.
अवश्य पढ़े,
| वर्ग का क्षेत्रफल | घन का आयतन |
| आयत का क्षेत्रफल | समानान्तर चतुर्भुज का क्षेत्रफल |
| समलम्ब चतुर्भुज का क्षेत्रफल | समचतुर्भुज का क्षेत्रफल |
| घनाभ का आयतन | निर्देशांक ज्यामिति फार्मूला एवं परिभाषा |
घन का फार्मूला
पूर्ण पृष्ठीय या पार्श्व का क्षेत्रफल के सभी घटक ज्ञात करने के लिए निम्न फार्मूला की सहायता लिया जाता है. ये फार्मूला किसी भी घनाकार आकृति का क्षेत्रफल निकालने के लिए प्रयुक्त होते है. जैसे;
घन का पार्श्वपृष्ठ का क्षेत्रफल = 4a2
घन का सम्पूर्ण पृष्ठ का क्षेत्रफल = 6a2
घन का विकर्ण = √3 × a
घन का एक किनारा = √ (सम्पूर्ण पृष्ठ का क्षेत्रफल / 6 )
पार्श्वपृष्ठ का एक किनारा = √ ( पार्श्वपृष्ठ का क्षेत्रफल / 4 )
आयतन = a3
जहाँ ” a ” घन की कनारा या भुजा है.
घन के क्षेत्रफल सम्बंधित फार्मूला
1. घन के प्रत्येक किनारा m गुना करने से पृष्ट के क्षेत्रफल m2 गुना बढ़ जाता है.
2. घन के प्रत्येक किनारा में x % की वृद्धि की जाए, तो क्षेत्रफल में ( 2 x2 + x / 100 ) % की वृद्धि होती है.
3. घन के प्रत्येक किनारा में x % की कमी की जाए, तो क्षेत्रफल में ( 2 x2 – x / 100 ) % की कमी होती है.
4. आयतन के मदद से घन का किनारा = विकर्ण की लम्बाई / √3
अवश्य पढ़े,
घन सम्बन्धी महत्वपूर्ण तथ्य
सामान्यतः घन एक वर्गाकार आकृति है जिसमे 6 समान सतह होते है. यहाँ घन का गुणधर्म के विषय कुछ तथ्य वर्णित है जो वास्तिविकता प्रदर्शित है.
- घन का आकार वर्गाकार पिंड के समान होता है. जिसमे,
- विकर्ण की संख्या = 4
- सतहों की संख्या = 6
- घन में शीर्ष की संख्या = 8
- किनारों की संख्या = 12
- घन में शीर्षकोणों की संख्या = 24
घन के क्षेत्रफल सम्बंधित उदाहरण
Q. 1. घन का सम्पूर्ण पृष्ठ का क्षेत्रफल ज्ञात करे, यदि इसके प्रत्येक किनारों की लम्बाई 10 cm है?
हल: दिया है, घन की एक किनारा = a = 10cm
सम्पूर्ण पृष्ठ का क्षेत्रफल = 6a2
=> 6 × 10 × 10
अर्थात, a = 600 वर्ग इकाई.
Q. 2. एक घनाकार दिवार को पेंट करने लगा कुल लागत ज्ञात करे, जहाँ घनाकार दिवार की लम्बाई 2 cm है तथा दीवान को पेंट करने की लगत 5 रु. प्रति सेमी मीटर है.
हल: दिवार की लम्बाई 2 cm
सम्पूर्ण पृष्ठ का क्षेत्रफल = 6a2
=> 6 × 2 × 2 = 24 cm2
अतः दिवार को पेंट कराने में लगा कुल लागत = 5 × 24 = 120 रुपया.
Q. 3. यदि घन का पार्श्वपृष्ट का क्षेत्रफल 100 cm2 हो, तो घन की भुजा निकाले?
हल: दिया है, पार्श्वपृष्ट का क्षेत्रफल = 100 cm2
फार्मूला से, 4a2 = 100
=> a2 = 25, => a = √ 25
इसलिए, a अर्थात, भुजा = 5 cm.
घनाकार आकृति से सम्बंधित Ghan ka Kshetrafal ज्ञात करने के लिए उपर दिए गए फार्मूला में से ही प्रयोग होता है. इससे भिन्न फार्मूला नही होता है. अतः उन्हें स्मरण रखे ताकि प्रश्न करने में परेशानी न हो.
पूछे जाने वाले प्रश्न: FAQs
घन का क्षेत्रफल का सूत्र 4a2 होता है. जहाँ a घन की प्रत्येक भुजा है.
घन का पृष्ठीय क्षेत्रफल घन के किनारों की लंबाई के वर्ग के छह गुणा के बराबर है. अर्थात, 6a2 पृष्ठीय क्षेत्रफल है, जहाँ अ घन की भुजा है.
घन के विकर्ण का फार्मूला √3a होता है, जहाँ a = घन की भुजा है.