निर्देशांक ज्यामिति फार्मूला एवं परिभाषा

Whatsapp Group

Telegram channel

निर्देशांक ज्यामिति को गणित की सबसे महत्वपूर्ण अवधारणाओं में से एक माना जाता है. क्योंकि ज्यामिति और अलजेब्रा के बीच के बक्र और रेखा से जुड़े ग्राफ के जरिए लिंक का वर्णन किया जाता है. Nirdeshank Jyamiti का अध्ययन क्लास 5 से ही शुरू हो जाता है और ग्रेजुएशन तक जारी रहता है.

हालांकि यह बीजगणित में ज्यामिती के विशेष पहलू को महत्व देता है. जिससे ज्यामितीय समस्याओं को हल करने में मदद मिलता है. निर्देशांक ज्यामिति बिंदुओं की स्थिति को एक क्रमबद्ध समूह की संख्या का उपयोग करके वर्णित करना सिखाता है. जिसमे फार्मूला एवं महत्वपूर्ण रूल्स सामिल होते है.

Table of Contents

निर्देशांक ज्यामिति की परिभाषा

परिभाषा: निर्देशांक ज्यामिति गणित की वह महत्वपूर्ण शाखा है जिसमें समतल आकृति पर बने बिन्दुओं की स्थिति को दो संख्याओं के जोड़े के रूप में परिभाषित किया जाता है. संख्याओं के जोड़ों से बने बिंदु की स्थिति को बिंदु निर्देशांक कहते हैं.

दुसरें शब्दों में, ज्यामितिय शाखाओं का वह समूह है, जहां निर्देशांक का उपयोग करके एक बिंदु की स्थिति को परिभाषित किया जाता है, वह निर्देशांक ज्यामिति कहलाता है.

Nirdeshank Jyamiti का प्रयोग किसी दो बिन्दुओं के बिच की दुरी, केंद्र से दुरी बिन्दुओं का विभाजन आदि करने के लिए किया जाता है.

अवश्य पढ़े,

त्रिकोणमिति फार्मूला और ट्रिक्स	वर्ग का महत्वपूर्ण क्षेत्रफल
वर्ग की परिभाषा और सूत्र	समानान्तर चतुर्भुज का क्षेत्रफल

निर्देशांक ज्यामिति के चतुर्थांश

XOX’ क्षैतिज अक्ष है. इसे x अक्ष भी कहते है.
YOY’ उर्ध्वादर अक्ष है. इसे y अक्ष भी कहते है.
XOX’ तथा YOY’ रेखाएं एक दुसरें को O बिंदु पर लम्बवत कटती है.

XOY तल को प्रथम चरण अथवा कोटि (Quadrant) कहते है.
X’OY तक को द्वितीय चरण कहते है.
X’OY’ तल को तृतीय चरण कहते है.
XOY’ तल को चतुर्थ चरण कहते है.

चतुर्थांश का चिन्ह

प्रथम पाद यानि चरण = ( +, + )
द्वितीय पाद = ( -, + )
तृतीय पाद = ( -, – )
चतुर्थ पाद = ( +, – )

अवश्य पढ़े, त्रिकोणमिति क्लास 10th सभी फार्मूला

नियामक: Nirdeshank Jyamiti

XX’ अक्ष का धन भाग = ( +, 0 )
XX’ का ऋण भाग = ( -, 0 )
YY’ अक्ष का धन भाग = ( 0, + )
YY’ अक्ष का ऋण भाग = ( 0, – )
मूल बिंदु = ( 0, 0 )

Note:
XX’ अक्ष के प्रत्येक बिंदु Y नियामक शून्य होता है.
YY’ अक्ष के प्रत्येक बिंदु पर x नियामक शून्य होता है.
मूल बिंदु पर x नियामक तथा y नियामक दोनों शून्य होते है.

अवश्य पढ़े, सामानांतर श्रेढ़ी का सभी फार्मूला

दुरी सूत्र | निर्देशांक ज्यामिति का सूत्र

एक बिंदु x- अक्ष और दूसरा बिंदु y- अक्ष पर स्थित किसी भी दो निर्देशांक बिंदु के बीच की दूरी ज्ञात के लिए निम्न फार्मूला का प्रयोग किया जाता है. दुरी सूत्र का प्रयोग क्लास 10th और 12th में अधिक प्रयोग होता है.

दूरी सूत्र (Distance formula) = √[(x2-x1)² + (y2-y1)²]

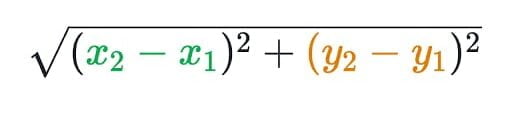
Note:

x₁ – रेखा के पहले बिंदु का x- निर्देशांक
x₂ – रेखा के दूसरे बिंदु का x- निर्देशांक
y₁ – रेखा के पहले बिंदु का y- निर्देशांक
y₂ – रेखा के दूसरे बिंदु का y- निर्देशांक

x- अक्ष पर स्थिर बिन्दुओं का निर्देशांक (x, 0) यानी y- निर्देशांक शून्य तथा y- अक्ष पर स्थिर बिन्दुओं का निर्देशांक (0, y) यानी x- निर्देशांक शून्य होता हैं और मूल बिंदु का निर्देशांक (0, 0) होता हैं.

इसे भी पढ़े, संख्या पद्धति फार्मूला एवं परिभाषा

मध्य बिंदु का सूत्र

किसी भी दो निर्देशांक बिंदु के बीच के मध्य निर्देशांक बिंदु ज्ञात करने के लिए मध्य बिंदु सूत्र की प्रयोग किया जाता है.

जहाँ, A कोई बिंदु है जिसका निर्देशांक A (x₁, y₁) है तथा दूसरा बिंदु B, जिसका निर्देशांक B (x₂, y₂) है. इस स्थति में मध्य बिंदु के निर्देशांक P (x, y) होगा.

x = (x₁ + x₂)/2
और
y = (y₁ + y₂) /2

P निर्देशांक = [ ( x₁ + x₂ )/2 , ( y₁ + y₂ )/2]

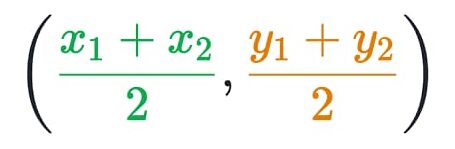
जहाँ

x₁ – रेखा के पहले बिंदु का x- निर्देशांक
x₂ – रेखा के दूसरे बिंदु का x- निर्देशांक
y₁ – रेखा के पहले बिंदु का y- निर्देशांक
y₂ – रेखा के दूसरे बिंदु का y- निर्देशांक

अवश्य पढ़े, द्विघात समीकरण फार्मूला

विभाजन सूत्र | निर्देशांक ज्यामिति का सूत्र

कोई बिंदु, किसी रेखा को किसी भी अनुपात में विभाजन करता है, तो उस बिंदु के निर्देशांक ज्ञात करने के लिए निम्न फार्मूला का प्रयोग किया जाता है.

विभाजन सूत्र क्लास 10th के साथ-साथ अन्य प्रतियोगिता परीक्षा में प्रयोग किया जाता है. क्योंकि यह निर्देशांक ज्यामिति का मुख्य आधार माना जाता है.

मान कि कोई रेखा A और B है, जिसमे A बिंदु के निर्देशांक A (x₁, y₁) और B बिंदु के निर्देशांक B (x₂, y₂) है, को m:n के रूप में विभाजित किया जाता है. तो इसे ज्ञात करने के लिए इस फार्मूला का प्रयोग होता है.

अवश्य पढ़े, बहुपद का सूत्र एवं परिभाषा

x = (m × x₂ + n × x₁) /m+n
और
y = (m × y₂ + n × y₁) /m+n, अर्थात

जहाँ

x₁ – रेखा के पहले बिंदु का x- निर्देशांक
x₂ – रेखा के दूसरे बिंदु का x- निर्देशांक
y₁ – रेखा के पहले बिंदु का y- निर्देशांक
y₂ – रेखा के दूसरे बिंदु का y- निर्देशांक
m – रेखा के विभाजन के अनुपात का पहला भाग
n – रेखा के विभाजन के अनुपात का दूसरा भाग

रेखा के विभाजन से प्राप्त बिंदु m:n के रूप का होगा.

निर्देशांक ज्यामिति में त्रिभुज का क्षेत्रफल

आमतौर पर त्रिभुज का क्षेत्रफल ज्ञात करने के लिए कई अन्य फार्मूला है लेकिन Nirdeshank Jyamiti में क्षेत्रफल निकालने के लिए विशेष फार्मूला का प्रयोग किया जाता है. जो इसके बिन्दुओं पर आधारित होता है.

सामान्य फार्मूला:
त्रिभुज का क्षेत्रफल = 1/2 × आधार × शीर्षलंब

लेकिन यदि निर्देशांक से बने त्रिभुज का क्षेत्रफल ज्ञात करना हो, तो इस फार्मूला का प्रयोग होता है.

माना कि किसी त्रिभुज के तीन बिन्दुएँ A, B, और C है, जिसका निर्देशांक A (x₁, y₁) , B (x₂, y₂) और C (x₃, y₃) है, तो त्रिभुज का क्षेत्रफल

∆ABC का क्षेत्रफल = 1/2[x₁(y₂–y₃) + x₂(y₃–y₁) + x₃(y₁–y₂)], अर्थात

जहाँ, A (x₁, y₁) , B (x₂, y₂) और C (x₃, y₃) त्रिभुज के निर्देशांक है.

निष्कर्ष

किसी तल पर किसी बिंदु की स्थिति निर्धारित करने के लिए , निर्देशांक के अक्षो के युग्म की आवश्यकता होती है. किसी बिंदु का y- अक्ष यानि y-axis से दूरी , उस बिंदु का x- निर्देशांक या भुज कहलाती है. किसी बिंदु की x- अक्ष से दूरी, उस बिंदु का y-निर्देशांक या कोटि कहलाती है.

इसी प्रकार, x- अक्ष पर स्थित किसी बिंदु के निर्देशांक (x, 0) तथा y- अक्ष पर स्थित किसी बिंदु के निर्देशांक (0, y) के रूप का होता है. उम्मीद करता हूँ की Nirdeshank Jyamiti से सम्बंधित अब कोई संदेह शेष नही होगा.