वर्ग की परिभाषा, फार्मूला एवं गुणधर्म | Varg ki Paribhasha

गणितज्ञों के विचारधारा के अनुसार, ज्यामिति में, एक वर्ग द्वि-आयामी समतल आकृति है, जिसमें चार समान भुजाएँ होती हैं, तथा वर्ग के सभी कोण 90 डिग्री के बराबर होते हैं. वर्ग के सभी पक्ष समान लम्बाई एवं समान कोण के समतल आकृति है जिसका गुणधर्म लगभग अन्य चतुर्भुज से थोड़ा-सा भिन्न होता है.

सामान्यतः आयत के गुण कुछ हद तक एक वर्ग के लगभग समान होता हैं, क्योंकि दोनों की आकृति लगभग समान ही होता है. आयत में केवल विपरीत भुजाएँ समान होती हैं, इसलिए, एक आयत को एक वर्ग कहा जा सकता है, जब उसके सभी चार हिस्से समान लंबाई के हों.

सभी आवश्यक Varg ki Paribhasha, गुणधर्म एवं वर्ग का विकर्ण, आदि का विस्तृत जानकरी यहाँ किया गया है जो ज्यामिति आपको आच्छा पकड़ बनाने में मदद करेगा.

वर्ग किसे कहते है: Varg ki Paribhasha

चार भुजाओं से घिरी वह बंद आकृति जिसकी चारों भुजाएं एक दुसरें से बराबर हों तथा चारों कोण समकोण यानी 90 डिग्री के हों, वह वर्ग कहलाता है.

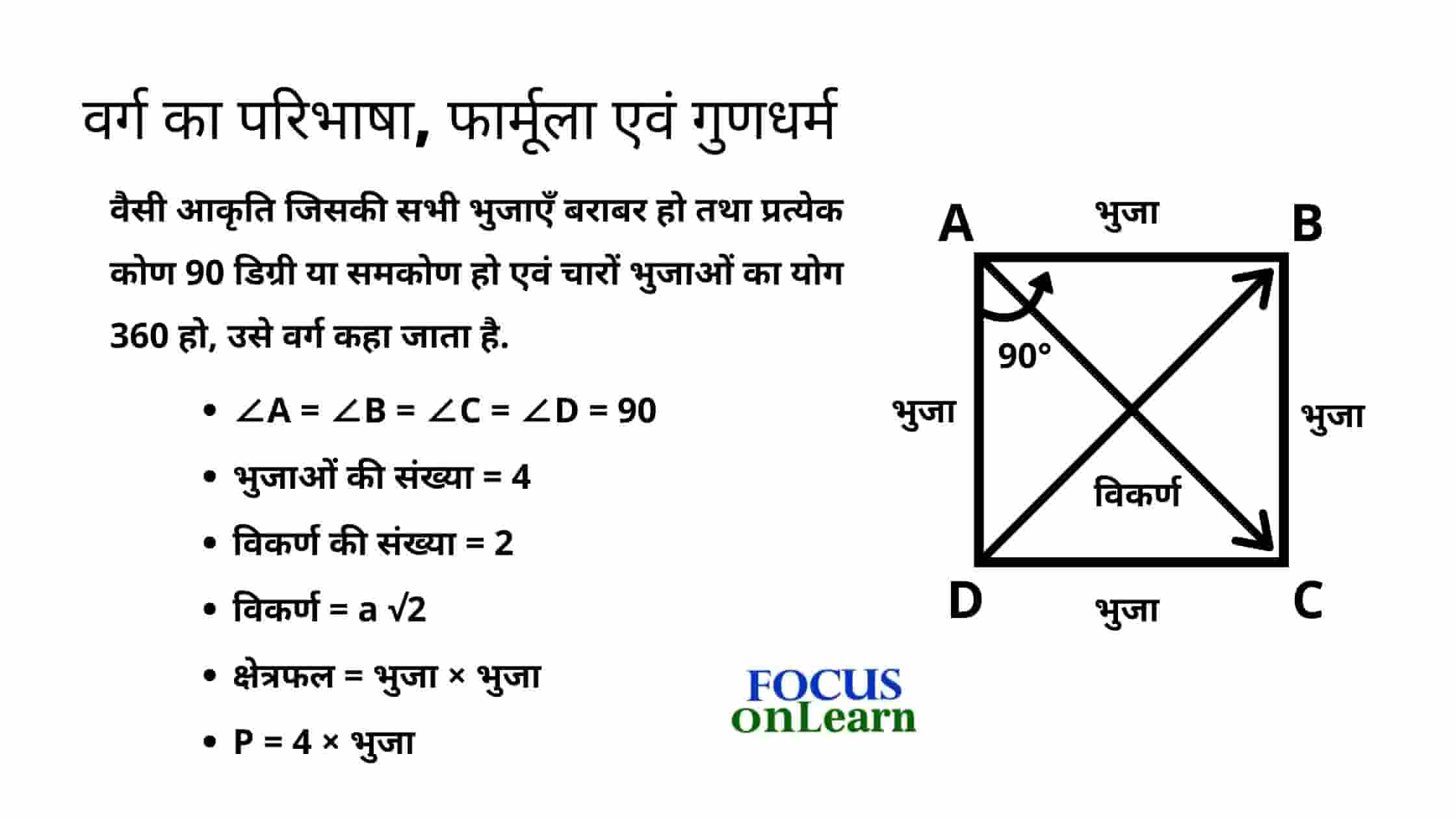
दुसरें शब्दों में, वैसी आकृति जिसकी सभी भुजाएँ बराबर हो तथा प्रत्येक कोण 90 डिग्री या समकोण हो एवं चारों भुजाओं का योग 360 हो, उसे वर्ग कहा जाता है.

साथ ही वर्ग के विकर्ण बराबर एक दुसरें के बराबर होते हैं तथा एक दूसरे को 90 डिग्री पर द्विभाजित करते हैं.

• ∠A + ∠B + ∠C + ∠D = 360
• ∠A = ∠B = ∠C = ∠D
• अर्थात सभी भुजाओं का माप बराबर हो.
• ∠A = ∠B = ∠C = ∠D = 90
• भुजाओं की संख्या = 4
• विकर्ण की संख्या = 2

Note:-
एक वर्ग को एक आयत के रूप में भी परिभाषित किया जा सकता है, जहां दो विपरीत भुजाओं की समान लंबाई हो, तथा कोण 90 डिग्री के बराबर हो.

वर्ग का विकर्ण

सामान्यतः वर्ग का विकर्ण एक ऐसा खण्ड है जो वर्ग के दो विपरीत शीर्षों को आपस में जोड़ता है. विकर्ण की लम्बाई दुसरें से समान एवं समरूप होता है. विकर्ण वर्ग की सबसे बड़ी भुजा होती है, जो वर्ग दो बराबर भागो में विभक्त करती है.

दुसरें शब्दों में, वर्ग में खींची गई सबसे लंबी रेखा को विकर्ण कहा जाता है.

वर्ग के विकर्ण का सूत्र

वर्गाकार आकृति में विकर्ण ज्ञात करने के लिए भुजाओं का मान ज्ञात होना अनिवार्य होता है. यदि किसी स्थति में भुजा नही दिया रहे, तो वर्ग का क्षेत्रफल या परिमाप से विकर्ण, निम्न फार्मूला का प्रयोग कर निकाला जा सकता है.

पाईथागोरस प्रमेय से, लम्ब = विकर्ण

• (कर्ण)² = (लम्ब)² + (आधार)²

• अर्थात, (विकर्ण)² = (भुजा)² + (भुजा)²

• => (विकर्ण)² = 2 (भुजा)² => (विकर्ण) = √2 (भुजा)²

अतः d = √2 (a)²

विकर्ण = a √2 

जहाँ a वर्ग की भुजा है.

• यदि भुजा ज्ञात नही हो और क्षेत्रफल या परिमाप दिया गया हो, तो
• A= भुजा × भुजा या 4 × a का प्रयोग कर
• पहले वर्ग की भुजा निकालने
• फिर वर्ग के विकर्ण फार्मूला से प्रश्न हल करे.

वर्ग का परिमाप और क्षेत्रफल

क्षेत्रफल और परिमाप वर्ग के प्रमुख दो गुण है जो इसे एक वर्ग के रूप में परिभाषित करता है. ऐसे फार्मूला का प्रयोग प्रश्न को हल करने के लिए अलग-अलग रूप किया जाता है.

वर्ग का क्षेत्रफल:

मुख्यतः वर्ग का क्षेत्रफल दो-आयामी विमाओं द्वारा घिराहुआ क्षेत्र है जो भुजाओं के वर्ग के बराबर होता है.

• क्षेत्रफल = भुजा × भुजा
• अर्थात, A = a², वर्ग इकाई

वर्ग का परिमाप:

वर्ग की परिधि इसके सभी चार भुजाओं के योग के बराबर होता है, अर्थात, चारों भुजाओं का जोड़ परिमाप है, तथा परिधि की इकाई वर्ग की लंबाई के समान होती है.

• परिमाप = भुजा + भुजा + भुजा + भुजा
• अर्थात, P = 4 × भुजा

वर्ग का गुणधर्म

• Varg चतुर्भुज का एक भाग है.
• इसमें चार कोण, चार शीर्ष एवं चार भुजा होती है.
• दो विकर्ण भी होते है जो वर्ग की सबसे बड़ी भुजा होती है.
• प्रत्येक कोणों का योग 360° होता है.
• चारों भुजाओं की लम्बाई आपस में बराबर होता है.
• प्रत्येक कोण समकोण होता है.
• विकर्ण एक दुसरें को समद्विभाग करते है.
• आमने सामने की भुजाएं बराबर और समांतर होती हैं.
• Varg के भुजाओं के मध्य-बिन्दुओं को आपस में मिलाने पर प्राप्त चतुर्भुज भी एक वर्ग होता है.
• वर्ग के विकर्ण 90° पर एक दूसरे से कटते हैं.
• वर्ग का विकर्ण इसे दो समान समद्विबाहु त्रिभुजों में विभाजित करता है.

महत्वपूर्ण तथ्य

Varg ki Paribhasha के अनुसार वर्ग को सम चतुर्भुज भी कहा जाता है. क्योकिं, सम चतुर्भुज में विपरीत भुजाएँ भी समान होती है. वर्ग एक चार भुजाओं वाला बहुभुज है, जिसकी लंबाई सभी भुजाओं के समान हैं. यहाँ सभी आवश्यक वर्ग की परिभाषा, सूत्र एवं गुणधर्म उपलब्ध है जितना किसी एग्जाम में जरुरत होता है. उम्मीद है आपको अवश्य पसंद आएगा.

पूछे जाने वाला सामान्य प्रश्न FAQs

Q. वर्ग के क्षेत्रफल का सूत्र क्या होता है?

वर्ग के क्षेत्रफल का सूत्र भुजा × भुजा अर्थात a x a = a² होता है.

Q. वर्ग के विकर्ण का सूत्र क्या होता है?

वर्ग के विकर्ण का सूत्र (कर्ण)² = (लम्ब)² + (आधार)² होता है.

jikeshkumar

जिकेश कुमार इस वेबसाइट के फाउंडर है जिन्हें लगभग 5 वर्षो का कंटेंट राइटिंग अनुभव है. इस वेबसाइट उपलब्ध सभी जानकारी दर्शकों के पसंद एवं जरुरतों को ध्यान में रखकर तैयार किया गया है. इस वेबसाइट पर एजुकेशन महत्वपूर्ण जानकारी के साथ लोन एवं स्कॉलरशिप, सरकारी योजना, स्टडी टिप्स की भी जानकारी प्राप्त होगी.