ज्यामितीय आकृति में Varg ka Parimap वह लंबाई है जो इसकी सम्पूर्ण सतह को कवर करती है. अर्थात भुजाओं से घिरा हुआ क्षेत्र परिमाप के अंतर्गत आता है. वर्ग का परिमाप, सभी भुजाओं को एक साथ जोड़कर प्राप्त किया जाता है. यह ज्यामिति का विशेष नियम है, जो लगभग हर आकृति में प्रयोग होता है.
परिस्थिति के अनुसार परिमाप का प्रयोग विभिन्न प्रकार के प्रशों को हल करने के लिए लगभग प्रतियोगिता एग्जाम, बोर्ड एग्जाम एवं अन्य सरकारी परीक्षा में होता है. यहाँ वर्ग के परिमाप से सम्बंधित सभी महत्वपूर्ण तथ्य उपलब्ध है. जो व्यक्तिगत उपयोग के साथ-साथ जनरल तैयारी में भी मदद करता है.
वर्ग का परिमाप क्या होता है?
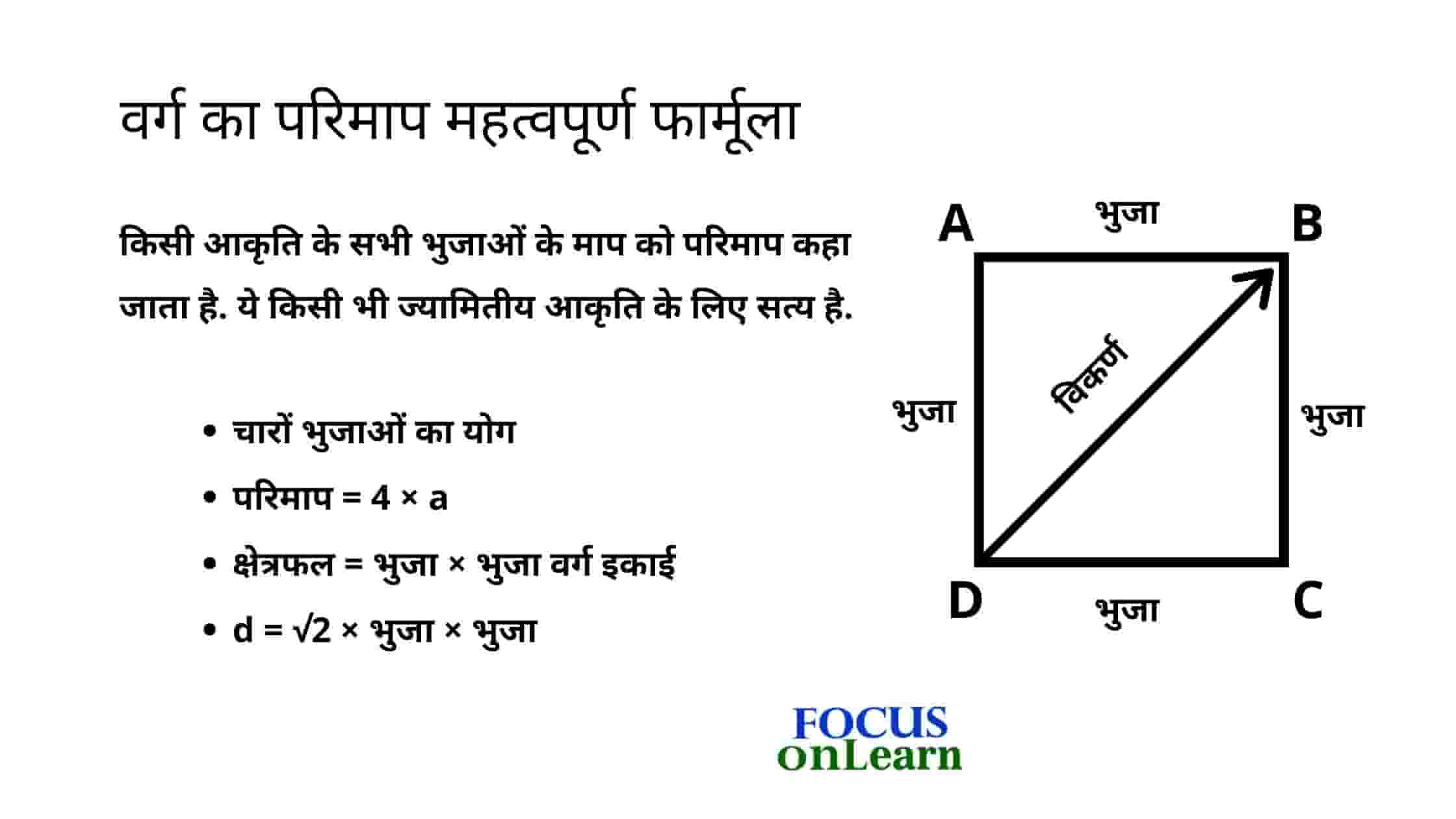
मुख्य रूप से, “परिमाप” दो शब्दो से मिलकर बना है. परि और माप, “परि” का अर्थ “चारों ओर” तथा “माप” का अर्थ “मापना” होता है. अर्थात, किसी आकृति के सभी भुजाओं के माप को परिमाप कहा जाता है. ये किसी भी ज्यामितीय आकृति के लिए सत्य है. जैसे वर्ग की परिमाप है.
किसी भी बंद ज्यामितीय आकृति की परिमाप को उस आकृति के आसपास की दूरी के रूप में गणितज्ञों द्वारा परिभाषित किया गया है. मुख्य रूप से, वर्ग का परिधि की गणना उसके चारों भुजाओं को जोड़कर ज्ञात किया जाता है.
हालांकि, वर्ग के सभी भुजाएँ आपस में समान होते हैं. इसलिए, इसकी परिधि इसके किनारे यानि भुजाओं के 4 गुनी होती है.
- ∠A = ∠B = ∠C = ∠D
- अर्थात सभी भुजाओं का माप बराबर हो.
- विकर्ण एक दुसरें से बराबर माप के होते है.
वर्ग का परिमाप का सूत्र
सामान्यतः वर्ग एक चतुर्भुज है और अन्य चतुर्भुज की तरह ही इसका भी परिमाप सभी भुजाओं के योग से ज्ञात किया जाता है. और क्षेत्रफल भुजाओं के गुणनफल से प्राप्त होता है. लेकिन यदि वर्ग में भुजा ज्ञात न हो, और विकर्ण दिया हो तो अन्य फार्मूला का प्रयोग कर परिमाप एवं क्षेत्रफल ज्ञात किया जाता है. जो इस प्रकार है;
अवश्य पढ़े,
| त्रिभुज के प्रकार और गुणधर्म | समबाहु त्रिभुज का फार्मूला एवं गुण |
| समद्विबाहु त्रिभुज का फार्मूला | समकोण त्रिभुज का क्षेत्रफल एवं गुण |
| विषमबाहु त्रिभुज फार्मूला | न्यूनकोण त्रिभुज फार्मूला |
वर्ग का परिमाप
Varg का परिमाप इसके भुजाओं का योग होता है. जैसे;
परिमाप = भुजा + भुजा + भुजा + भुजा
=> चारों भुजाओं का योग
=> परिमाप = 4 × भुजा
अर्थात, परिमाप = 4 × a
जहाँ a वर्ग के प्रत्येक भुजा की लम्बाई है.
वर्ग का क्षेत्रफल
सामान्यतः वर्ग के क्षेत्रफल को द्वि-आयामी आकृति के वर्ग यानि (भुजा × भुजा) में परिभाषित किया जाता है. क्योंकि अन्य चतुर्भुज के समान भुजाओं का गुणनफल ही क्षेत्रफल होता है.
क्षेत्रफल = भुजा × भुजा वर्ग इकाई
अर्थात, A = a2, वर्ग इकाई
यदि किसी स्थति में भुजा के बदले विकर्ण दिया हो, तो d = √2 (a)2 का प्रयोग कार पहले भुजा ज्ञात करे उसके बाद वर्ग का परिमाप निकाले.
वर्ग के परिमाप से सम्बंधित उदाहरण
1. यदि किसी वर्ग के प्रत्येक भुजा की लम्बाई 10 cm हो, तो परिमाप निकाले?
हल: दिया है, भुजा = 10 cm
इसलिए, परिमाप = 4 × a
=> P = 4 × 10 => P = 40 cm
2. यदि किसी वर्ग का विकर्ण 2 cm हो, तो वर्ग की परिधि ज्ञात करे?
हल: दिया है, विकर्ण = 2 cm
इसलिए, d = √2 (a)2
अर्थात, 2 = √2 (a)2
=> 2 / √2 = a2
चूँकि 2 को इस प्रकार लिखा जा सकता है. (√2)2
=> (√2)2/√2 = a2
(√2)2/√2 को कटाने पर शेष 2 बचेगा.
यानि 2 = a2, इसलिए a = √2
अतः परिमाप = 4 × a => 4 × √2
परिमाप = 4√2. उत्तर
अवश्य पढ़े,
| आयत का परिमाप | आयत का क्षेत्रफल और परिभाषा |
| समानान्तर चतुर्भुज का क्षेत्रफल | समलम्ब चतुर्भुज का क्षेत्रफल |
| त्रिकोणमिति क्लास 10th सभी फार्मूला | अलजेब्रा का फार्मूला |
महत्वपूर्ण निष्कर्ष
Varg ka Parimap चतुर्भुज का सबसे महत्वपूर्ण भाग है, जिसमे अलग-अलग प्रकार के प्रश्न पूछे जाते है. ऊपर एक ऐसा उदहारण दिया गया है. जो लगभग दुसरें प्रश्न से पूरी तरह अलग है. अगर विद्यार्थी वर्ग के परिमाप, क्षेत्रफल, विकर्ण एवं परिभाषा को अच्छे से ध्यान रखे, तो किसी भी तरह के प्रश्न को सरलता हल कर सकते है. ऐसे प्रश्न का उदेश्य केवल विद्यार्थियों में मन में प्रेरणा जागृत करना है कि वे कैसे भी प्रश्न को चुटकी में सोल्व कर लेंगे.
पूछे जाने वाला समान्य प्रश्न FAQs
Q. वर्ग का परिमाप फार्मूला क्या होता है?
वर्ग का परिमाप फार्मूला, भुजा + भुजा + भुजा + भुजा अर्थात, 4 × a होता है.
Q. वर्ग का क्षेत्रफल का फार्मूला क्या होता है?
वर्ग का क्षेत्रफल फार्मूला A = a2, वर्ग इकाई होता है.