छिन्नक शंकु का वह भाग है. जब इसे किसी समतल द्वारा दो भागों में काटा जाता है, तब छिन्नक प्राप्त होता है. शंकु का ऊपरी भाग आकार में समान रहता है, लेकिन नीचे का भाग एक छिन्नक बनाता है. यह एक प्रकार का ग्लासनुमा आकृति होता है, जो शंकु के दो बराबर भाग में काटने पर प्राप्त होता है. यही भाग छिन्नक फार्मूला में सर्वाधिक प्रयोग होता है.
शंकु का छिन्नक एक लैटिन शब्द है जिसका शाब्दिक अर्थ “टुकड़ा” होता है. छिन्नक प्राप्त करने के लिए किसी ठोस को इस तरह से काटा जाता है कि ठोस का आधार और ठोस को काटने वाला तल एक दूसरे के समानांतर हो. तथा ठोस का वह हिस्सा जो समानांतर काटने वाले भुजा और आधार के बीच स्थिर हो.
उदाहरणस्वरुप, एक ग्लास को शंकु के छिन्नक के रूप में परिभाषित किया जा सकता है. यह क्लास 10, 11 और 12 के लिए सर्वाधिक महत्वपूर्ण टॉपिक है. क्योंकि, इससे प्रत्येक एग्जाम में कम से कम 5% तक प्रश्न होते है. इसलिए, छिन्नक का फार्मूला को ध्यान से पढ़ना अनिवार्य है.
| बेलन का आयतन | घन का आयतन |
| त्रिज्यखंड का क्षेत्रफल | त्रिकोणमिति परिचय |
| द्विघात समीकरण फार्मूला | समचतुर्भुज का क्षेत्रफल |
| घनाभ का आयतन | निर्देशांक ज्यामिति फार्मूला |
छिन्नक किसे कहते है?
जब एक शंकुनुमा आकृति को किसी समतल द्वारा दो भागों में काटने पर प्राप्त नए त्रिआयामी आकृति को शंकु का छिन्नक कहा जाता है. प्राप्त त्रिआयामी आकृति का केंद्र, वृत्त और त्रिज्याएँ समनांतर एवं समरूप होती है.
अर्थात, शंकु का वह रूप जो तिकोना न हो, बल्कि ग्लास के आकृति के समरूप हो, वह छिन्नक कहलाता है.
- छिन्नक में दो वृत्त, केंद्र एवं दो त्रिज्या होती है.
- शंकु को काटने पर ही छिन्नक प्राप्त होता है.
- तिर्यक ऊंचाई शंकु के समरूप होते है.
- ऊंचाई = h
- ऊपर की त्रिज्या = R
- आधार की त्रिज्या = r
- तिर्यक ऊंचाई l
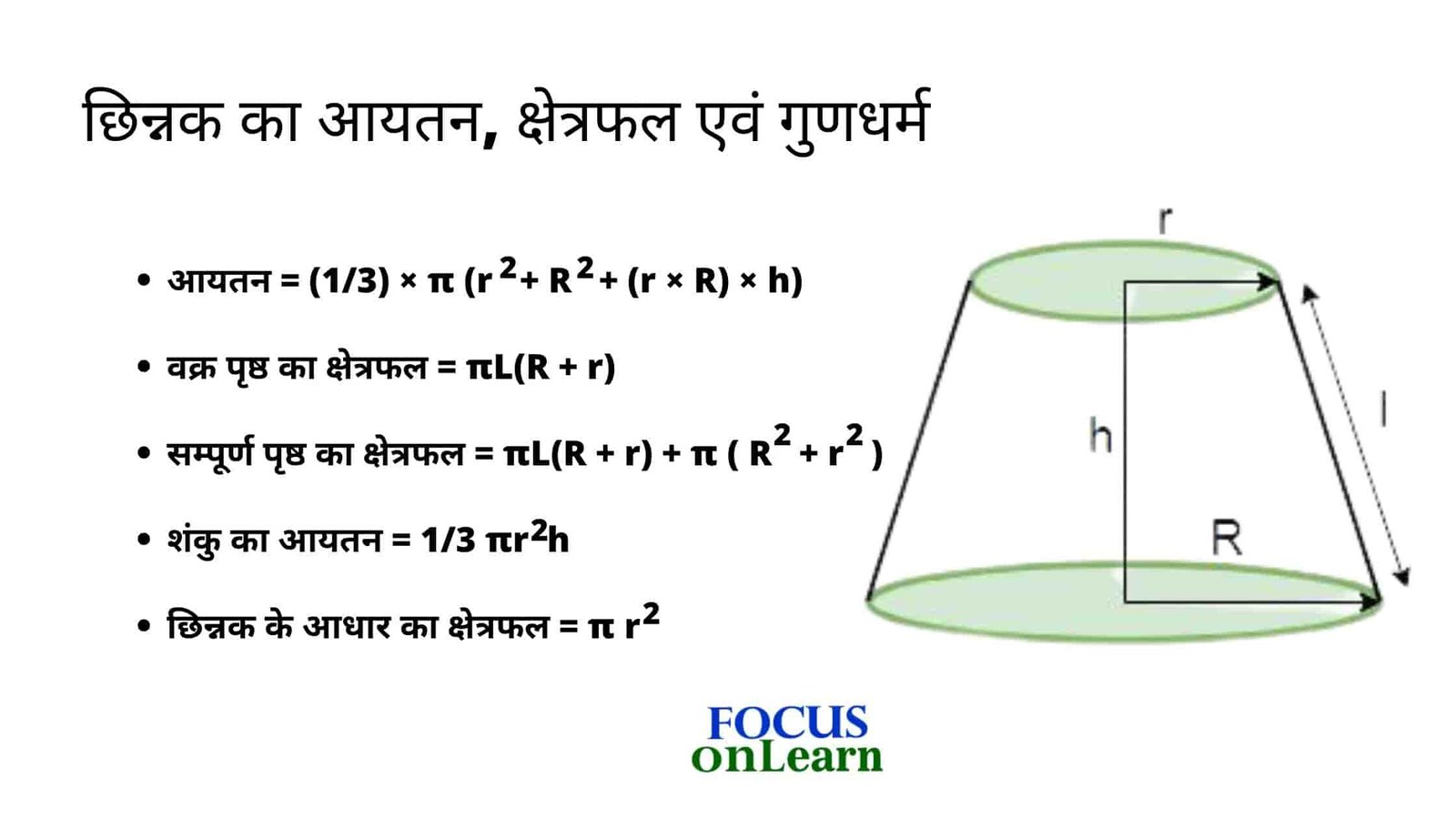
छिन्नक का आयतन का सूत्र
शंकु का वह भाग जो ग्लासनुमा त्रिआयामी आकृति के रूप का है. उसका आयतन ज्ञात करने के लिए निम्न फार्मूला का प्रयोग किया जाता है.
शंकु के छिन्नक का आयतन = (1/3) × π (r2 + R2 + (r × R) × h)
जहाँ,
- ऊंचाई = h
- ऊपर की त्रिज्या = R
- आधार की त्रिज्या = r, है.
शंकु का आयतन = 1/3 πr2h
अवश्य पढ़े, शंकु के आयतन के महत्वपूर्ण तथ्य
छिन्नक के वक्र पृष्ठीय क्षेत्रफल
शंकु के छिन्नक का वक्र पृष्ठ क्षेत्रफल एवं सम्पूर्ण वक्र पृष्ठीय क्षेत्रफल में थोड़ी से भिन्नता होती है. जिसे समझना अत्यंत आवश्यक है. ये हमेशा confusion पैदा करता है. इसलिए, छिन्नक से सम्बन्धित क्षेत्रफल का Frustum Formula यहाँ अलग-अलग दिया गया है.
छिन्नक का वक्र पृष्ठ का क्षेत्रफल = πL(R + r)
जहाँ, l = √ (h2 +(R-r)2 )
शंकु के छिन्नक का सम्पूर्ण पृष्ठ का क्षेत्रफल = वक्र पृष्ठ का क्षेत्रफल + दोनों वृत्त के आधार का क्षेत्रफल
=> πL(R + r) + πR2 + πr2
छिन्नक का सम्पूर्ण पृष्ठ का क्षेत्रफल = πL(R + r) + π ( R2 + r2 )
शंकु के छिन्नक का गुण
- छिन्नक के दो वृताकार आधारों के बीच ऊंचाई समलम्ब होती है.
- बड़े वृत्त की त्रिज्या को R तथा छोटे त्रिज्या को r माना जाता है.
- शंकु की ऊंचाई, जिसमे छिन्नक बनाया गया है = (hr / r – R)
- शंकु का तिर्यक ऊंचाई, जिसमे छिन्नक बनाया गया है = (lr / r – R)
छिन्नक सम्बंधित उदाहरण
Q. यदि किसी छिन्नक की ऊंचाई 5 cm, तिर्यक ऊँचाई 4, बड़ी त्रिज्या 3cm और छोटी त्रिज्या 2cm हो, तो छिन्नक का सम्पूर्ण वक्र पृष्ठ का क्षेत्रफल एवं आयतन ज्ञात करे.
Solution: दिया है, h = 5 cm, l = 4cm, r = 3cm और R = 2cm, तो
छिन्नक का सम्पूर्ण पृष्ठ का क्षेत्रफल = πL(R + r) + π ( R2 + r2 )
=> 22/7 × 4 × (2 + 3 ) + 22/7 ( 4 + 9 )
= 440/7 + 286/7 = 720/ 7 = 348.8 वर्ग इकाई
छिन्नक का आयतन = (1/3) × π (r2 + R2 + (r × R) × h)
=> 1/3 × [ 22/7 ( 9 + 4 + (3 + 2 ) × 5)
= 1/ 3 × 22/7 × 34 = 748/21 घन इकाई
पूछे जाने वाले सामन्य प्रश्न FAQs
Q. छिन्नक के सभी सूत्र बताएं
उत्तर: शंकु के छिन्नक में बहुत सारे फार्मूला का प्रयोग होता है. लेकिन जिस फार्मूला का सर्वाधिक उपयोग होता है वो ये है.
- शंकु का छिन्नक का आयतन = (1/3) × π (r2 + R2 + (r × R) × h)
- छिन्नक का वक्र पृष्ठ का क्षेत्रफल = πL(R + r)
- छिन्नक का सम्पूर्ण पृष्ठ का क्षेत्रफल = πL(R + r) + π ( R2 + r2 )
Q. छिन्नक का वक्र पृष्ठ क्षेत्रफल क्या होता है?
उत्तर: वक्र पृष्ट एवं सम्पूर्ण पृष्ठ के क्षेत्रफल में अंतर होता है. और इसी में विद्यार्थी गलती कर देते है. इसलिए, फार्मूला को ध्यान से देखें.
छिन्नक का वक्र पृष्ठ का क्षेत्रफल = πL(R + r), जहाँ l तिर्यक ऊँचाई है.
Q. गिलास का आयतन कैसे निकाले?
उत्तर: ग्लास एक प्रकार का छिन्नक है. जिसका आयतन निकालने के लिए Frustum का आयतन का फार्मूला का प्रयोग होता है. इसमें त्रिज्याएँ भिन्न भिन्न होती है. अतः त्रिज्या के बड़े और छोटे रूप को ध्यान में रख कर फार्मूला का प्रयोग करे.
ग्लास का आयतन = (1/3) × π (r2 + R2 + (r × R) × h)
गणित से सम्बंधित फार्मूला
| वृत्त का परिभाषा एवं फार्मूला | बहुभुज की परिभाषा एवं फार्मूला |
| चतुर्भुज का सभी क्षेत्रफल | त्रिभुज का सभी क्षेत्रफल |
| बेलन का आयतन | क्षेत्रमिति के सभी फार्मूला |
यहाँ Chhinnak ka Formula के सभी आवश्यक भाग उपलब्ध है. यदि इसके अतिरिक्त भी किसी फार्मूला की आवश्यकता हो, तो कृपया कमेंट करके हमें अवश्य बताएँ.